Kalman Filter :: Applications in Finance
Noise in data refers to any unwanted or irrelevant information that interferes with the transmission or processing of a signal. In signal processing, the goal is to extract the useful information (the signal) from the noise. This can be particularly challenging in scenarios like wireless communication, where signals are transmitted through the air and can be distorted or contaminated by various environmental factors. Techniques such as filtering and noise reduction are used to mitigate the effects of noise and recover the original signal as accurately as possible.
The concept of noise extends to various domains such as data science and finance, where raw data typically contains valuable information, like trading signals, amidst irrelevant noise. Extracting and distinguishing this meaningful data from extraneous noise presents a significant challenge, particularly when the true signal is unknown.
The Kalman filter stands out as a powerful tool in dynamic linear modeling, particularly for analyzing sequential data like time series. Unlike traditional methods such as moving averages or exponential moving averages, which rely on fixed-size windows or predetermined weights, the Kalman filter dynamically adjusts its estimates based on incoming information. It does so by incorporating new data into its calculations, continually updating its predictions of the current state of the time series through a probabilistic framework.
Specifically, the Kalman filter operates as a probabilistic model that accounts for a sequence of observations, denoted as \(z_{1}, z_{2}, …, z_{T}\), and their corresponding hidden states, represented as \(x_{1}, x_{2}, …, x_{T}\). This model iteratively refines its estimates of the hidden states by recursively applying two main steps: prediction and update. In the prediction step, the filter forecasts the next state based on the previous state and the system dynamics. Then, in the update step, it assimilates the most recent observation, refining its prediction based on the observed data and its associated uncertainty.
By dynamically adjusting its estimates in response to new information, the Kalman filter excels in scenarios where data evolves over time and where accurately tracking the underlying process is paramount. Its versatility and adaptability make it a cornerstone in various fields, including engineering, finance, and robotics, where real-time decision-making relies on precise and up-to-date information.
The Kalman filter is a powerful algorithm designed to leverage noisy observations of a system over time, enabling real-time estimation of its parameters, some of which may be unobservable, and forecasting future observations. At each time step, it performs prediction, measurement intake, and self-updating based on the comparison between prediction and measurement.
The filter prioritizes high-accuracy estimates, crucial for making precise predictions and informed decisions. Consequently, it finds extensive application in robotics and real-time systems where dependable information is indispensable.
Notably, the Kalman filter excels in efficiently estimating future state variables within nonlinear prediction systems. Regarded as an optimal estimator, it proves particularly valuable in predictive model development, especially when dealing with limited dataset sizes.
How does it work?
The algorithm operates as follows.
- Input Parameters - Receive a mathematical model of the system comprising:
- The transition matrix (commonly denoted as \(A\)), indicating the system’s evolution from one state to another. For example, in modeling a car’s movement, kinematic equations could compute the subsequent position and velocity based on prior values. Alternatively, for a stable system, a random walk model might suffice.
- The observation matrix (typically denoted as \(H\)), specifying the expected next measurement based on the predicted state. In simpler cases like measuring a car’s position, it might directly extract position values from the state. In more complex scenarios such as linear regression, the state represents model coefficients, and the next measurement is predicted from the linear equation.
- Any control factors influencing state transitions but not directly measured (summarized in matrix B and time-varying control vector \(u_{t}\)).
- Covariance matrices for transition noise (Q) and measurement noise (R).
- Initial Estimation:
- Accept an initial estimate (\(μ_{0}\)) of the system state and its estimation error (\(σ_{0}\)).
- At each timestep:
- Estimate the current system state (\(x_{t}\)) using the transition matrix.
- Receive new measurements (\(z_{t}\)).
- Update the current state estimate (\(x_{t}\)) and its covariance matrix (\(P_{t}\)) by considering the conditional probability of measurements given the state, while factoring in uncertainties in both measurement and state estimation.
The Kalman filter relies on the following assumptions to effectively recover the hidden state:
- Linearity: The system under consideration behaves linearly.
- Markovian Property: The hidden state process follows a Markov chain, meaning that the current state (\(x_{t}\)) depends solely on the most recent prior state (\(x_{t-1}\)).
- Gaussian Noise: Measurements are affected by Gaussian, uncorrelated noise with a constant covariance.
Hence, the Kalman filter shares similarities with a hidden Markov model (HMM), albeit with some key distinctions. In the Kalman filter, the latent variable’s state space is continuous, and both hidden and observed variables follow normal distributions, typically denoted with mean \(\mu\) and standard deviation \(\sigma\).
Assuming the following linear equation for evolution of the state: \(X_{k} = F_{k} X_{k−1} + W_{k}\)
where:
\(X_{k}\) is the true state at time \(t_{k}\),
\(F_{k}\) is the state transition matrix assumed to be time dependent,
\(W_{k}\) is the process noise assumed to be a multivariate normal distribution with zero mean and covariance \(Q_{k}\), that is, \(W_{k} ∼ N(0,Q_{k})\).
The following Python code example shows how to apply the Kalman filter to smoothen the Apple stock price series for the 2019-21 period.
stock_prices = us_stock_prices['AAPL']['Close'].loc['2019':'2021']
Kalman filter can be applied using pykalman in Python. I initialize the Kalman Filter with unit covariance matrices and zero means.
from pykalman import KalmanFilter
kf = KalmanFilter(transition_matrices = [1],
observation_matrices = [1],
initial_state_mean = 0,
initial_state_covariance = 1,
observation_covariance=1,
transition_covariance=.01)
Then, I run the filter method to trigger the forward algorithm, which iteratively estimates the hidden state, that is, the mean of the time series:
s_means, _ = kf.filter(stock_prices)
Finally, add moving averages for comparison and plot the result:
# Compare with moving average
stock_prices_smoothed = stock_prices.to_frame('Close')
stock_prices_smoothed['Kalman Filter'] = s_means
for months in [1,2,3]:
stock_prices_smoothed[f'MA ({months}m)'] = stock_prices.rolling(window=months*33).mean()
ax = stock_prices_smoothed.plot(title='Kalman Filter vs Moving Average', figsize=(14,6), lw=1, rot=0)
ax.set_xlabel('')
ax.set_ylabel('Chosen Stock')
plt.tight_layout()
sns.despine();
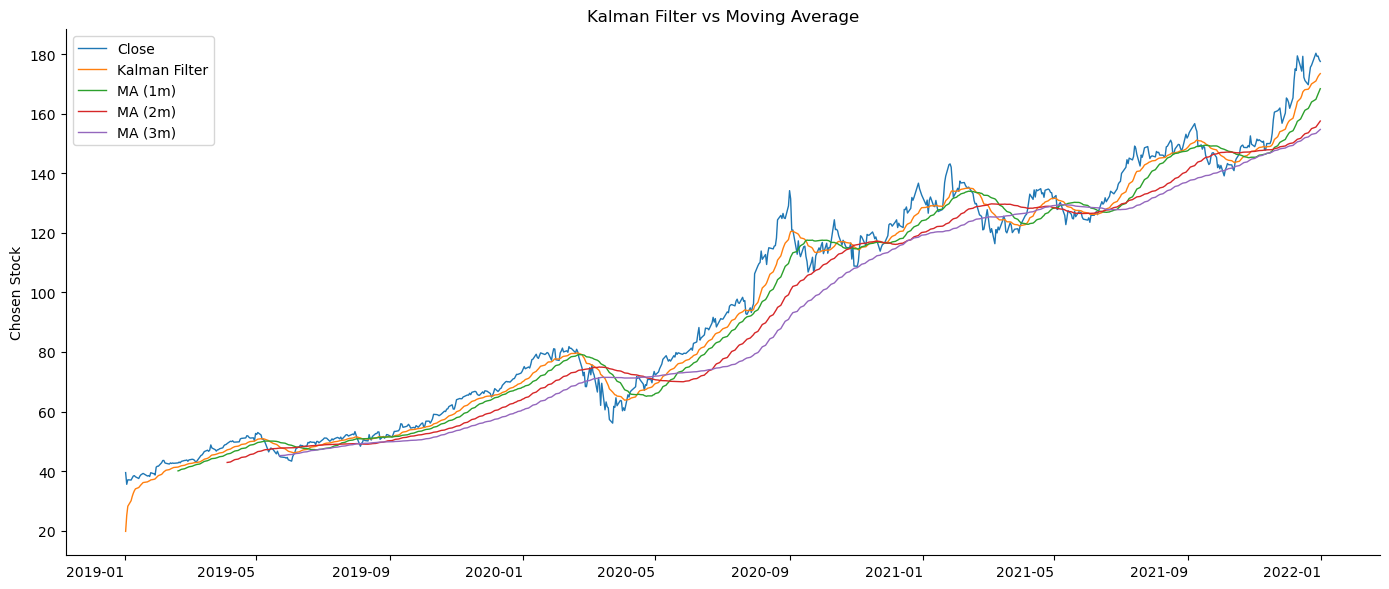
The resulting plot above shows that the Kalman filter performs similarly to a 1-month moving average but is more sensitive to changes in the behavior of the time series.
The Kalman filter is particularly useful for rolling estimates of data values or model parameters that change over time. This is because it adapts its estimates at every time step based on new observations and tends to weigh recent observations more heavily. Unlike conventional moving averages, the Kalman filter does not require us to specify the length of a window used for the estimate. Rather, we start out with our estimate of the mean and covariance of the hidden state and let the Kalman filter correct our estimates based on periodic observations.
Key disadvantages are the assumptions of linearity and Gaussian noise that financial data often violates and as we know in reality, in a temporal and spatial time-series of financial data (e.g. stock prices) there are common nonlinearities.
The basic Kalman filter is meant for linear systems, but it can be adapted to model non-linear transition and observation functions effectively. To handle such cases, Extended Kalman Filters (EKF) and Unscented Kalman Filters (UKF) are used, with the latter conveniently integrated into pykalman. These filters are capable of handling scenarios where noise is not simply additive, such as when it’s proportional to the measurement’s size. Moreover, they allow for the specification of non-Gaussian errors, a particularly useful feature when dealing with financial data, which often exhibits heavy-tailed distributions.
The Extended Kalman Filter (EKF) and Unscented Kalman Filter (UKF) are heuristic approaches to using Kalman filtering for nonlinear systems.
When the system dynamics and observation models are highly nonlinear, the UKF can be an improvement over the EKF. The UKF is based on the unscented transformation, which is a method for computing the statistics of a random variable \(x\) that undergoes a nonlinear transformation \((y = g(x))\). The random variable \(x\) is sampled using a carefully chosen set of sigma points and these sample points are propagated through the nonlinear function \(g\).
The UKF tends to be more robust and accurate than the EKF but has higher computation overhead due to the sampling process.
References:
- Dixon, M. F., Halperin, I., & Bilokon, P. (2020). Machine Learning in Finance. Springer.
- A. Javaheri, D. Lautier, and A. Galli. Wilmott Magazine, 2003 (3): 67–83 (2003)
- Guo, M., & Zhang, Q. (2021). Machine Learning for Asset Management: A Primer. Journal of Portfolio Management, 47(2), 114-128.